Abschnitt 3 TRD 301 Anlage 1 - Einzelspannungen (1)
3.1. Ideal-elastische mechanische Lochrandspannungen
3.1.1.
Die maximale Lochrandspannung für Zylinderschalen mit senkrechten Abzweigen wird nach folgender Beziehung ermittelt:
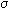 ip =
ip = 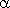 m × p* dm/2sb (2)
m × p* dm/2sb (2)
Für die Formzahl 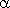 m gilt
m gilt
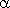 m =
m = 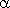 m0 + fu ×
m0 + fu × 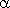 b (3)
b (3)
Falls 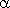 m bzw. die Formzahl
m bzw. die Formzahl 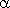 m0 weder durch Messungen noch durch Rechnung bestimmt wurden, ist einzusetzen:
m0 weder durch Messungen noch durch Rechnung bestimmt wurden, ist einzusetzen:
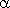 m0 = 2,6 m0 = 2,6
| für durchgesteckte und durchgeschweißte Abzweige, Bild 1, sowie für im Gesenk geschmiedete Abzweige mit kegeligem Übergang und Ausrundung, Bilder 2 und 3, jeweils ohne Restspalt |
|---|---|
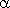 m0 = 2,9 m0 = 2,9
| für aufgeschweißte Abzweige; Aufsatzfläche angepaßt oder ebengefräst; Wurzel ausgebohrt oder überschliffen, ohne Restspalt, Bild 4 |
| Abweichend hiervon kann für | |
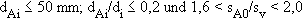 | |
die Formzahl 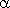 m0 = 2,4 gesetzt werden m0 = 2,4 gesetzt werden
| |
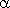 m0 = 3,2 m0 = 3,2
| für ausgehalste Grundkörper mit angeschweißtem Abzweig; Wurzel ausgebohrt oder überschliffen, ohne Restspalt, Bild 5 |
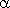 m0 = 5,0 m0 = 5,0
| für Walz- oder Walz/Schweißverbindungen |
Sind die Anforderungen an die Schweißverbindung nicht erfüllt, z.B. bei unbearbeiteter Schweißwurzel oder einem Restspalt <= 1,5 mm, so ist 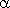 m0 um den Faktor für den Einfluß des Wurzelspaltes
m0 um den Faktor für den Einfluß des Wurzelspaltes
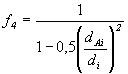 (4)
(4)
zu erhöhen. Bei Durchmesserverhältnissen dAi/di; > 0,5 und zugleich di > 300 mm sind jedoch die Anforderungen nach (1) grundsätzlich einzuhalten. Wurzelspalte >1,5 mm sind unzulässig.
(2) Falls die Formzahl 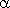 b weder durch Messungen noch durch Rechnung bestimmt wurde, gilt für alle Abzweige
b weder durch Messungen noch durch Rechnung bestimmt wurde, gilt für alle Abzweige 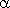 b = 2,0.
b = 2,0.
(3) Unrundheitsfaktor fu für elliptische Formabweichung. Bild 6,
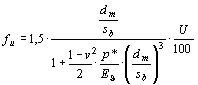 (5)
(5)
3.1.2.
Zylinderschalen mit schrägen und/oder nicht radial angeordneten Abzweigen sind vorerst noch Nummer 3.1.1 zu berechnen.
3.1.3.
Lochfelder in Zylinderscholen werden bei dieser Betrachtung wie Einzelausschnitte
noch Nummer 3.1.1 behandelt.
3.1.4.
Zylinderschalen mit Y-förmigen Abzweigen unter dem Öffnungswinkel 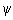 A sind vorerst wie folgt zu berechnen:
A sind vorerst wie folgt zu berechnen:
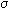 ip =
ip = 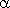 m × p* dm/2sb (6)
m × p* dm/2sb (6)
Hierin ist einzusetzen:
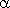 m = 2,5 + (90-
m = 2,5 + (90-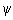 A)2 / 1000 (7)
A)2 / 1000 (7)
jedoch nicht weniger als 3,2.
Eine Schweißnahtwurzel im Zwickelbereich ist zu bearbeiten; falls dies nicht möglich ist, ist 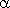 m mit f4 = 1,2 zu multiplizieren
m mit f4 = 1,2 zu multiplizieren
3.2 Ideal-elastische Lochrand-Wärmespannungen
Diese Spannungen hängen nur vom radialen Temperaturverlauf in der Behälterwand ab. Für die Innenwand gilt unter der Annahme eines rotationssymmetrischen Temperaturverlaufs (auch bei Thermoschock)
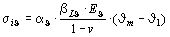 (8)
(8)
Hierin ist die Formzahl 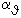 = 2 einzusetzen, es sei denn, daß ein anderer Wert rechnerisch nachgewiesen wird.
= 2 einzusetzen, es sei denn, daß ein anderer Wert rechnerisch nachgewiesen wird.
Unter der Voraussetzung eines quasistationären Temperaturverlaufs bei isolierter Außenwand wird die Temperaturdifferenz 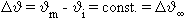 und kann wie folgt als Funktion der Temperaturänderungsgeschwindigkeit
und kann wie folgt als Funktion der Temperaturänderungsgeschwindigkeit 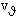 angegeben werden:
angegeben werden:
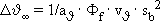 (9)
(9)
Hier ist  f ein Farmfaktor nach Bild 7.
f ein Farmfaktor nach Bild 7.
Für die meßtechnische Überwachung kann 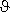 m mit ausreichender Genauigkeit in der Mitte der Wand gemessen werden.
m mit ausreichender Genauigkeit in der Mitte der Wand gemessen werden.
