Abschnitt 8.2 - 8.2 Berechnung gemäß DIN EN 12195-1:2011-06
8.2.1
Berechnung der Ladungssicherungsmaßnahmen durch Formschluss gemäß DIN EN 12195-1:2011-06
Beispiel: Lkw, Baujahr 2008, zGM 7,5 t, Kofferaufbau gemäß DIN EN 12642 (Code L)
Rechenbeispiel 1
Sicherung in Fahrtrichtung, Reibbeiwert μ = 0,2
Nutzlast des Fahrzeugs (NL) 5.000 kg
Gewichtskraft der Ladung (FG) 5.000 daN
Reibbeiwert μ = 0,2
(kein Einsatz von rutschhemmendem Material)
| Nach vorn zu sichernde Kräfte | 80 % FG | = | 4.000 daN |
|---|---|---|---|
| Belastbarkeit der Stirnwand | - 40 % NL | = | - 2.000 daN |
| Reibungskraft | - 0,2 FG | = | - 1.000 daN |
| Differenzkraft, die noch zu sichern ist | = | 1.000 daN | |
| Bei formschlüssiger Beladung ist die Ladungssicherung nach vorn nicht erfüllt. |
|---|
Ohne Anti-Rutsch-Matten
Abb. 8-2
Formschlüssig beladener Lkw ohne ARM
Rechenbeispiel 2
Sicherung in Fahrtrichtung, Reibbeiwert μ = 0,6
Nutzlast des Fahrzeugs (NL) 5.000 kg
Gewichtskraft der Ladung (FG) 5.000 daN
Reibbeiwert μ = 0,6
(Einsatz von rutschhemmendem Material)
| Nach vorn zu sichernde Kräfte | 80 % FG | = | 4.000 daN |
|---|---|---|---|
| Belastbarkeit der Stirnwand | - 40 % NL | = | - 2.000 daN |
| Reibungskraft | - 0,6 FG | = | - 3.000 daN |
| Differenzkraft, die noch zu sichern ist | = | 0 daN * | |
| Bei formschlüssiger Beladung ist die Ladungssicherung nach vom erfüllt; damit ist gleichzeitig auch die Ladungssicherung zur Seite und nach hinten erfüllt, da die Beschleunigungskräfte nach vom am größten sind. |
|---|
Mit Anti-Rutsch-Matten
Abb. 8-3
Formschlüssig beladener Lkw mit ARM
| Der Einsatz von rutschhemmendem Material bewirkt, dass in Rechenbeispiel 2 die Ladung ausreichend gesichert ist. |
|---|
Rechenbeispiel 3
Sicherung nach hinten
Nutzlast des Fahrzeugs (NL) 5.000 kg
Gewichtskraft der Ladung (FG) 5.000 daN
Reibbeiwert μ = 0,2
(kein Einsatz von rutschhemmendem Material)
| Rückwärtig zu sichernde Kräfte | 50 % FG | = | 2.500 daN |
|---|---|---|---|
| Belastbarkeit des Heckportals | - 25 % NL | = | - 1.250 daN |
| Reibungskraft | - 0,2 FG | = | - 1.000 daN |
| Differenzkraft, die noch zu sichern ist | = | 250 daN | |
| Bei formschlüssiger Beladung ist die Ladungssicherung nach hinten nicht erfüllt. |
|---|

Abb. 8-4
Formschlüssig beladener Lkw ohne ARM
Rechenbeispiel 4
Sicherung zur Seite, standfestes Ladegut
Nutzlast des Fahrzeugs (NL) 5.000 kg
Gewichtskraft der Ladung (FG) 5.000 daN
Reibbeiwert μ = 0,2
(kein Einsatz von rutschhemmendem Material)
| Seitlich zu sichernde Kräfte | 50 % FG | = | 2.500 daN |
|---|---|---|---|
| Belastbarkeit der Seitenwand | - 30 % NL | = | - 1.500 daN |
| Reibungskraft | - 0,2 FG | = | - 1.000 daN |
| Differenzkraft, die noch zu sichern ist | = | 0 daN * | |
| Bei formschlüssiger Ladung ist die Ladungssicherung seitlich erfüllt. |
|---|

Abb. 8-5
Formschlüssig beladener Lkw ohne ARM, Ansicht von hinten
| Bei den Rechenbeispielen 1 bis 4 handelt es sich um Musterberechnungen, die auf den durch die Normen vorgegebenen Prüfbelastungen beruhen. |
|---|
8.2.2
Berechnung der Ladungssicherungsmaßnahmen durch Niederzurren gemäß DIN EN 12195-1:2011-06
| Beim Niederzurren wird die Ladung durch die Zurrmittel auf die Ladefläche gepresst. |
|---|
Niederzurren eignet sich nur für formstabile Ladungen.
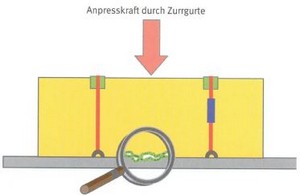
Abb. 8-6
Prinzipzeichnung Niederzurren
Das Zurrmittel wird in Zurrpunkten an der Ladefläche eingehängt, über die formstabile Ladung geführt und mit der Ratsche gespannt. Damit sich die Vorspannkräfte gleichmäßiger verteilen, sollten Kantengleiter verwendet werden.
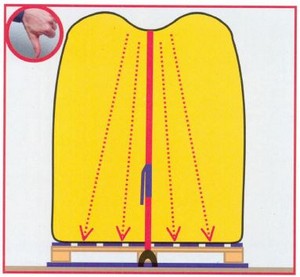
Abb. 8-7
Für eine nicht formstabile Ladung ist Niederzurren nicht geeignet.
Eine freistehende Ladung ist mit mindestens zwei Zurrgurten zu sichern, um ein Drehen der Ladung zu verhindern.
Die Ratschen sollten möglichst wechselseitig angebracht werden, um unterschiedliche Vorspannkräfte auszugleichen.
Wirksame Vorspannkraft FT gesbeim Niederzurren
Voraussetzungen für eine optimale Vorspannkraft sind u. a.:
Eine hohe, durch die Ratsche erzeugte Vorspannkraft (STF)
Ein formstabiles Ladegut
Der Einsatz von Kantengleitern
Ein Zurrwinkel α von fast 90°
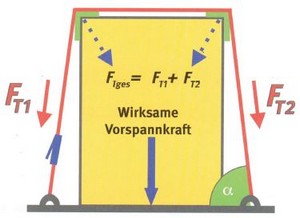
Abb. 8-8
Wirksame Vorspannkraft beim Niederzurren
| FT ges | = | Gesamtvorspannkraft des Zurrmittels in der Überspannung (wirksame Vorspannkraft, mit der die Ladung kraftschlüssig auf die Ladefläche gepresst wird) |
|---|---|---|
| FT 1 | = | Vorspannkraft im Zurrmittel auf der Seite der Ratsche |
| FT 2 | = | Vorspannkraft im Zurrmittel auf der Seite, die der Ratsche gegenüberliegt |
Auf der Seite der Ladung, die der Ratsche des Zurrgurts gegenüberliegt, ist die Vorspannkraft im Allgemeinen geringer. Der Grund dafür liegt im Reibungsverlust bei der Umlenkung des Zurrmittels an den Ladungskanten, der trotz Kantenschutz auftritt.
Die Sicherung nicht standfester Ladegüter hat in zwei Schritten zu erfolgen:
|
|---|
| Soll ein seitlich nicht standfestes Ladegut durch Niederzurren gesichert werden, müssen die verwendeten Zurrmittel gleichzeitig beide Funktionen erfüllen. |
|---|
Einfluss des Zurrwinkels α auf die Vorspannkraft
Die beim Niederzurren wirksame Vorspannkraft hängt u. a. vom Vertikalwinkel α des Zurrmittels ab.
Ein Zurrwinkel α von 90° bis 83° erzielt eine optimale Vorspannkraft des Zurrmittels und muss bei der Berechnung nicht berücksichtigt werden.
Ein Zurrwinkel α von unter 83° muss bei der Berechnung berücksichtigt werden.
Ein Zurrwinkel α von unter 30° sollte beim Niederzurren vermieden werden.
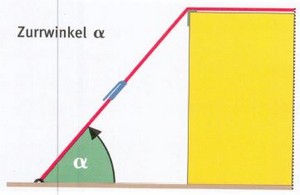
Abb. 8-9
Der Zurrwinkel α wird von der Ladefläche hoch zum Zurrmittel gemessen.
| Je flacher der Zurrwinkel α ist, desto weniger Vorspannkraft wirkt auf die Ladung und desto mehr Zurrmittel sind erforderlich. Bei einem Zurrwinkel α von 90° wirkt die Vorspannkraft zu 100 %. Bei einem Zurrwinkel α von 30° wirkt die Vorspannkraft nur noch zu 50 %. |
|---|
Mit vereinfachten Formeln kann die Anzahl der erforderlichen Zurrmittel berechnet werden.
Formel zur Ermittlung der Anzahl von Zurrmitteln
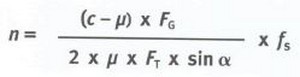
| n = Anzahl der erforderlichen Zurrmittel c = Beschleunigungsbeiwert μ = Reibbeiwert FG = Ladungsgewicht in daN FT = Vorspannkraft des Zurrmittels sin α = Sinuswert des Zurrwinkels α fs = Sicherheitsbeiwert, 1,25 in Fahrtrichtung 1,1 zur Seite, nach hinten |
|---|
Tabelle 22 Einfluss des Zurrwinkels auf die wirksame Vorspannkraft des Zurrmittels (sin α = Sinuswert des Zurrwinkels)
| Zurrwinkel | Sinus | Wirksame Vorspannkraft des Zurrmittels |
|---|---|---|
| 90° | 1 | 100 % |
| 80° | 0,98 | 98 % |
| 70° | 0,94 | 94 % |
| 60° | 0,87 | 87 % |
| 50° | 0,77 | 77 % |
| 40° | 0,64 | 64 % |
| 30° | 0,50 | 50 % |
| 20° | 0,34 | 34 % |
| 10° | 0,17 | 17 % |
Beispiel: Berechnungen für eine Ladung mit einer Gewichtskraft von 24.000 daN, mit Zurrmitteln STF= 500 daN
Rechenbeispiel 1
Sicherung nach vorne, ohne Anti-Rutsch-Matten
| Gewichtskraft der Ladung Zurrwinkel | c | = | 0,8 |
|---|---|---|---|
| μ | = | 0,3 | |
| FG | = | 24.000 daN | |
| α | = | 80°, sin α = 0,98 | |
| fs | = | 1,25 (Fahrtrichtung) |
Anzahl der Zurrmittel berechnen

Erforderlich: 51 Zurrmittel
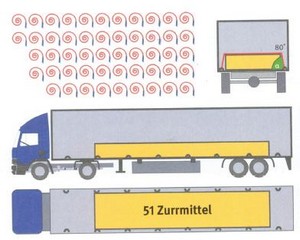
Abb. 8-10 bis 8-29
Die Abbildungen auf den Seiten 114 und 115 zeigen die jeweilige Beladesituation und die Anzahl der benötigten Zurrgurte.
Rechenbeispiel 2
Sicherung nach vorne, mit Anti-Rutsch-Matten
| Gewichtskraft der Ladung Zurrwinkel | c | = | 0,8 |
|---|---|---|---|
| μ | = | 0,6 | |
| FG | = | 24.000 daN | |
| α | = | 80°, sin α = 0,98 | |
| fs | = | 1,25 (Fahrtrichtung) |
Anzahl der Zurrmittel berechnen

Erforderlich: 11 Zurrmittel
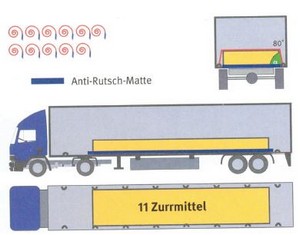
Anm.: Aus Gründen des Lastverteilungsplans ist in den Beispielen 1 und 2 eine formschlüssige Beladung nach vorne nicht möglich. Wenn möglich, sollte eine formschlüssige Ladungssicherung bevorzugt werden.
Beispiel: Berechnungen für eine Ladung mit einer Gewichtskraft von 24.000 daN, mit Zurrmitteln STF= 500 daN
Rechenbeispiel 3
Sicherung seitlich und nach hinten, ohne Anti-Rutsch-Matten
| Gewichtskraft der Ladung Zurrwinkel | c | = | 0,5 |
|---|---|---|---|
| μ | = | 0,3 | |
| FG | = | 24.000 daN | |
| α | = | 80°, sin α = 0,98 | |
| fs | = | 1,1 (zur Seite, nach hinten) |
Der Reibbeiwert von μ = 0,3 wurde der normativen Tabelle entnommen.
Anzahl der Zurrmittel berechnen

Erforderlich: 18 Zurrmittel
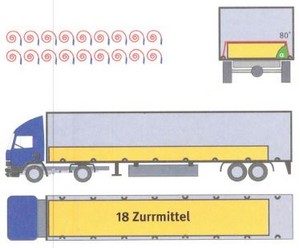
Rechenbeispiel 4
Sicherung seitlich und nach hinten, ohne Anti-Rutsch-Matten
| Gewichtskraft der Ladung Zurrwinkel | c | = | 0,5 |
|---|---|---|---|
| μ | = | 0,3 | |
| FG | = | 24.000 daN | |
| α | = | 30°, sin α = 0,5 | |
| fs | = | 1,1 (zur Seite, nach hinten) |
Der Reibbeiwert von μ = 0,3 wurde der normativen Tabelle entnommen.
Anzahl der Zurrmittel berechnen

Erforderlich: 36 Zurrmittel
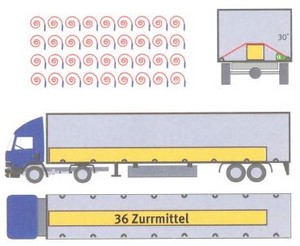
| Die beiden Beispiele zeigen den großen Einfluss des Zurrwinkels auf die Ladungssicherung. Aufgrund der erforderlichen hohen Anzahl an Zurrmitteln sind die Beispiele nicht praxisgerecht. Es wird dringend empfohlen Anti-Rutsch-Matten einzusetzen, um die Anzahl der erforderlichen Zurrmittel zu reduzieren. |
|---|
8.2.3
Berechnung der Ladungssicherungsmaßnahmen durch Diagonalzurren gemäß DIN EN 12195-1:2011-06
Diagonalzurren standfester Ladeeinheiten
| Diagonalzurren ist eine Art des Direktzurrens. Jedes Zurrmittel sichert die Ladung in zwei Richtungen. Die Rückhaltekraft der Zurrmittel wird durch die Zurrwinkel beeinflusst. |
|---|
Es wird mit zwei symmetrisch angeordneten Zurrmitteln pro Richtung gesichert.
Vor dem Berechnen sind bei jedem Zurrmittel die Zurrwinkel α und β zu messen.
Werden bei den verschiedenen Zurrmitteln unterschiedliche Zurrwinkel gemessen, ist mit den ungünstigsten dieser Zurrwinkel zu rechnen.
Formel zur Berechnung der Rückhaltekraft in Längsrichtung
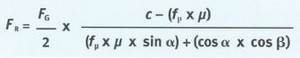
| c | = | 0,8 zur Sicherung in Fahrtrichtung für die hinteren Zurrmittel |
|---|---|---|
| c | = | 0,5 zur Sicherung entgegen der Fahrtrichtung für die vorderen Zurrmittel |
Formel zur Berechnung der Rückhaltekraft in Querrichtung
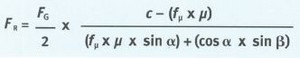
| FR | = | Rückhaltekraft für jedes Zurrmittel |
|---|---|---|
| FG | = | Gewichtskraft der Ladung |
| c | = | Beschleunigungsbeiwert |
| μ | = | Reibbeiwert |
| fμ | = | Umrechnungsfaktor für Reibbeiwert fμ = 0,75 (fμ = 1,0 bei Einsatz von RHM mit μ = 0,6) |
| α | = | Vertikalwinkel |
| sin α | = | Sinuswert des Zurrwinkels α |
| cos α | = | Cosinuswert des Zurrwinkels α |
| β | = | Horizontalwinkel |
| sin β | = | Sinuswert des Zurrwinkels β |
| cos β | = | Cosinuswert des Zurrwinkels β |
Rechenbeispiele für die Praxis
| Nachfolgend werden Musterberechnungen zur Ladungssicherung durch Diagonalzurren vorgestellt. Bei der Ladung handelt es sich um eine in einer Holzkiste verpackte Maschine. Anhand der Musterberechnungen soll verdeutlicht werden, wie sich die Verwendung von Anti-Rutsch-Matten auf die erforderlichen Rückhaltekräfte auswirkt. |
|---|
Die Zurrmittel wurden für beide Berechnungsbeispiele wie in der folgenden Grafik dargestellt, angelegt. Die Zurrwinkel betragen α = 40° und β = 30°
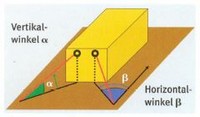
Abb. 8-30
Winkelbereiche beim Diagonalzurren
Tabelle 23 Sinus- und Cosinuswerte der Zurrwinkel
| Zurrwinkel | Sinus | Cosinus |
|---|---|---|
| 90° | 1 | 0 |
| 80° | 0,98 | 0,17 |
| 70° | 0,94 | 0,34 |
| 60° | 0,87 | 0,50 |
| 50° | 0,77 | 0,64 |
| 40° | 0,64 | 0,77 |
| 30° | 0,50 | 0,87 |
| 20° | 0,34 | 0,94 |
| 10° | 0,17 | 0,98 |
Bei den verwendeten Zurrmitteln handelt es sich um Schwerlastgurte mit einer LC von 5.000 daN im geraden Zug. Die Belastbarkeit der Zurrpunkte beträgt ebenfalls 5.000 daN.

Abb. 8-31
Zurrgurtetikett eines Schwerlast: gurts mit einer LC von 5.000 daN
| Die Rückhaltekraft FRdarf den auf dem Zurrgurtetikett angegebenen Wert für die zulässige Zurrkraft (LC) im geraden Zug nicht übersteigen. |
|---|
Beispiel: Berechnungen für die Sicherung einer standfesten Ladung mit einer Gewichtskraft von 24.000 daN
Rechenbeispiel 1: Sicherung ohne Anti-Rutsch-Matte
Der Lkw führt 4 Schwerlastgurte je LC= 5.000 daN mit.
| c | = | 0,8 bzw. 0,5 | |
|---|---|---|---|
| μ | = | 0,3 | |
| fμ | = | 0,75 | |
| Gewichtskraft der Ladung | FG | = | 24.000 daN |
| Vertikalwinkel | α | = | 40° |
| sin α | = | 0,64 | |
| cos α | = | 0,77 | |
| Horizontalwinkel | β | = | 30° |
| sin β | = | 0,50 | |
| cos β | = | 0,87 |
Berechnung der erforderlichen Rückhaltekraft in Fahrtrichtung

Berechnung der erforderlichen Rückhaltekraft nach hinten

Berechnung der erforderlichen Rückhaltekraft zu den Seiten

Erforderliche Rückhaltekraft je Zurrmittel:
In Fahrtrichtung 8.478 daN
Entgegen der Fahrtrichtung 4.055 daN
Zu den Seiten 6.238 daN
Zur Sicherung der Ladung sind folgende Zurrmittel erforderlich:
Hintere Zurrmittel (Sicherung in Fahrtrichtung und seitlich): LC mindestens 8.478 daN
Vordere Zurrmittel (Sicherung entgegen der Fahrtrichtung und seitlich): LC mindestens 6.238 daN
Rechenbeispiel 2: Sicherung mit Anti-Rutsch-Matte, μ = 0,6
Der Lkw führt 4 Schwerlastgurte je LC = 5.000 daN mit.
| c | = | 0,8 bzw. 0,5 | |
|---|---|---|---|
| μ | = | 0,6 | |
| fμ | = | 1,0 (RHM mit μ = 0,6) | |
| Gewichtskraft der Ladung | FG | = | 24.000 daN |
| Vertikalwinkel | α | = | 40° |
| sin α | = | 0,64 | |
| cos α | = | 0,77 | |
| Horizontalwinkel | β | = | 30° |
| sin β | = | 0,50 | |
| cos β | = | 0,87 |
Berechnung der erforderlichen Rückhaltekraft in Fahrtrichtung

Berechnung der erforderlichen Rückhaltekraft nach hinten

Berechnung der erforderlichen Rückhaltekraft zu den Seiten

| * Hinweis: | Negative Ergebnisse bedeuten, dass die Ladungssicherung erfüllt ist. Zur Vereinfachung werden negative Ergebnisse zu "0" gesetzt. |
|---|
| Die beiden Rechnungen haben ergeben, dass durch den Einsatz von Anti-Rutsch-Matten die mitgeführten Schwerlastgurte mit LC = 5.000 daN ausreichend sind. Die Anti-Rutsch-Matten müssen der Druckbelastung standhalten. |
|---|
8.2.4
Berechnung der Ladungssicherungsmaßnahmen durch Schlingenzurren gemäß DIN EN 12195-1:2011-06
| Schlingenzurren ist eine besondere Art des Direktzurrens. Dabei wird zwischen Kopfschlingenzurren
und Umreifungszurren unterschieden. In der Praxis sind diese Formen der Ladungssicherung
oft notwendig, weil keine Befestigungspunkte an der Ladung vorhanden sind. Die Berechnung des Schlingenzurrens ist sehr anspruchsvoll. Zur Vereinfachung können die nebenstehenden Tabellen verwendet werden. |
|---|
Vor dem Berechnen sind bei jedem Zurrmittel die Zurrwinkel α und β zu messen.
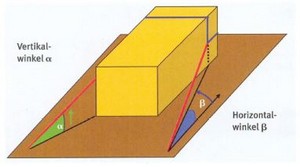
Abb. 8-32
Winkelbereiche beim Schlingenzurren
Die Kopfschlinge ist nach vorn mit einem Beschleunigungsbeiwert von c = 0,8 und nach hinten mit c = 0,5 zu berechnen.
Die Umreifungsschlinge ist mit einem Beschleunigungsbeiwert von c = 0,5 zu berechnen.
Es muss eine ausreichende Anzahl entsprechend belastbarer Zurrpunkte und Zurrmittel vorhanden sein.

Abb. 8-33
Zurrgurtetikett eines Spanngurts mit einer LC von 2.500 daN
Beim Schlingenzurren ist die zulässige Zurrkraft (LC) des Zurrmittels entscheidend.
Tabelle
"Rückhaltekraft beim Schlingenzurren"
Die nachfolgenden Tabellen zeigen, welche Gewichtskraft eine Ladung maximal haben darf, damit sie durch Schlingenzurren mit einem Zurrgurt in der Umreifung gesichert werden kann. Es wird von einer Belastbarkeit der Zurrpunkte LC von 2.000 daN je Zurrpunkt ausgegangen. Damit ergibt sich eine Rückhaltekraft der Schlinge von 4.000 daN. Ausgehend von dieser immer gleich angenommenen Rückhaltekraft wird die Gewichtskraft der Ladung bestimmt, die bei den jeweilig angegebenen Reibbeiwerten und Zurrwinkeln gesichert werden kann.
Tabelle 24
Berechnung und Reibbeiwert μ gemäß DIN EN 12195-1:2011
| μ = 0,2 | In Fahrtrichtung (FR) * | Entgegen und quer zur FR * | ||||
|---|---|---|---|---|---|---|
| β = 5° | β = 20° | β = 45° | β = 5° | β = 20° | β = 45° | |
| α = 30° | 5.771 | 5.470 | 4.230 | 10.717 | 10.158 | 7.856 |
| α = 45° | 4.988 | 4.742 | 3.730 | 9263 | 8.806 | 6.926 |
| α = 60° | 3.865 | 3.691 | 2.975 | 7.177 | 6.854 | 5.525 |
| μ = 0.3 | In Fahrtrichtung (FR) * | Entgegen und quer zur FR * | ||||
|---|---|---|---|---|---|---|
| β = 5° | β = 20° | β = 45° | β = 5° | β = 20° | β = 45° | |
| α = 30° | 6.784 | 6.444 | 5.043 | 14.185 | 13.473 | 10.544 |
| α = 45° | 6.007 | 5.729 | 4.585 | 12.560 | 11.979 | 9.587 |
| α = 60° | 4.821 | 4.624 | 3.815 | 10.079 | 9.668 | 7.977 |
| μ = 0.6 | In Fahrtrichtung (FR) * | Entgegen und quer zur FR * | ||||
|---|---|---|---|---|---|---|
| β = 5° | β = 20° | β = 45° | β = 5° | β = 20° | β = 45° | |
| α = 30° | 12.431 | 11.872 | 9.570 | Keine Rückhaltekraft erforderlich. Nur Fixieren gegen Wandern. | ||
| α = 45° | 11.687 | 11.230 | 9.351 | |||
| α = 60° | 10.146 | 9.824 | 8.494 | |||
| Beispiel: | Bei einem Reibbeiwert von μ = 0,3 und einem Zurrwinkel β von 5° kann durch die Rückhaltekraft der Kopfschlinge bei einem Zurrwinkel α von 30° in Fahrtrichtung eine Ladung mit einer Gewichtskraft von 6.784 daN gesichert werden. |
|---|---|
| Bei einem Zurrwinkel α von 60° beträgt die Gewichtskraft der Ladung nur noch 4.821 daN. |
| *Hinweis; | Negative Ergebnisse bedeuten, dass die Ladungssicherung erfüllt ist und weitere Kräfte aufgenommen werden könnten. Zur Vereinfachung werden negative Ergebnisse zu "0" gesetzt. |
|---|
| *Hinweis: | Negative Ergebnisse bedeuten, dass die Ladungssicherung erfüllt ist und weitere Kräfte aufgenommen werden könnten. Zur Vereinfachung werden negative Ergebnisse zu "0" gesetzt. |
|---|
Angegebene Werte = Gewichtskraft der Ladung in daN
